离散型流匹配模型（3）

接着上次说的DFM的分解技巧，继续学习DFM的最后一部分——混合路径（Mixture paths）。

混合路径（Mixture paths）

我们在此前的文章里面已经讲解了分解技巧¹，得到了分解的（边缘/条件）概率路径、分解的（边缘/条件）速率，以及知道了他们之间的关系（¹中的命题2和定理16）。现在我们要着手设计出一个具体的DFM了，类似FM²一样，我们可以从分解条件概率路径着手，然后得到目标分解条件速率，使用神经网络预测分解条件速率，最后使用分解CDFM损失（¹中公式14）来训练模型。

我们以$Z=(X_0,X_1) \sim \pi_{0,1}(X_0,X_1)$为条件（$X_0$和$X_1$为任意配对），那么分解的条件概率路径可以使用如下形式：

这个做法类似Rectified Flow（³中公式1），只是使用了更general的$\kappa_t$作为系数，$\kappa : [0,1] \to [0,1]$就类似扩散模型里面的噪声调度器，$\kappa_t \in C^1([0,1])$。根据¹中公式6，我们能得到非分解的条件概率路径：

关于公式1的详细解释：

分解概率路径上的随机变量$X_t^i \sim p_{t\mid 0,1}^i(\cdot\mid x_0,x_1) $满足：

\[X_t^i = \begin{cases} x_1^i \quad 概率为\kappa_t\\ x_0^i \quad 概率为(1-\kappa_t) \end{cases} \tag{3}\]

也就是对$t$时刻的第$i$个token $X_t^i$，它要么取源状态的值$x_0^i$，要么取目标状态的值$x_1^i$，取这两个值的概率与时间$t$相关。

从公式1和2给出的条件概率路径可以算出边缘概率路径，即：

需要指出的是，$p_t(x)$需要满足边缘条件，即$p_0(x) = \delta(x,x_0)$，$p_1(x) = \delta(x,x_1)$。为实现这个条件，需要让$\kappa_0 = 0$，$\kappa_1 = 1$。

接下来，我们需要知道公式1所示分解条件概率路径对应的分解条件速率$u_t^i(y^i,x^i\mid x_0,x_1)$。由Kolmogorov方程可知：

结合公式1给出的具体分解条件概率路径，可以算出：

关于（*）步的解释如下：

这里其实就是要证明

\[\delta(y^i,x_1^i) - p^i_{t\mid 0,1}(y^i\mid x_0,x_1) = \sum_{x^i} \left[ \delta(y^i,x_1^i) - \delta(y^i,x^i) \right] p^i_{t\mid 0,1}(x^i\mid x_0,x_1) \tag{7}\]

我们从右边开始变换：

\[\begin{aligned} \sum_{x^i} \left[ \delta(y^i,x_1^i) - \delta(y^i,x^i) \right] p^i_{t\mid 0,1}(x^i\mid x_0,x_1) &= \sum_{x^i} \left[ \delta(y^i,x_1^i)p^i_{t\mid 0,1}(x^i\mid x_0,x_1) - \delta(y^i,x^i)p^i_{t\mid 0,1}(x^i\mid x_0,x_1) \right]\\ &= \sum_{x^i} \delta(y^i,x_1^i)p^i_{t\mid 0,1}(x^i\mid x_0,x_1) - \sum_{x^i} \delta(y^i,x^i)p^i_{t\mid 0,1}(x^i\mid x_0,x_1) \\ &\overset{(1)}{=} \sum_{x^i} \delta(y^i,x_1^i)p^i_{t\mid 0,1}(x^i\mid x_0,x_1) - p^i_{t\mid 0,1}(y^i\mid x_0,x_1) \\ &\overset{(2)}{=} \delta(y^i,x_1^i) - p^i_{t\mid 0,1}(y^i\mid x_0,x_1) \\ \end{aligned} \tag{8}\]

第（1）步是delta函数的性质，$\int_x\delta(y,x)f(x)\mathrm{d}x = f(y)$，第（2）步是因为$\delta(y^i,x_1^i)$与$x^i$无关，$\sum_{x^i} p^i_{t\mid 0,1}(x^i\mid x_0,x_1) = 1 $。

对比公式6的最后结果和公式5，就知道：

这样我们就知道了公式1所示的分解条件概率路径对应的分解条件速率$u_t^i(y^i,x^i\mid x_0,x_1)$的具体形式了。

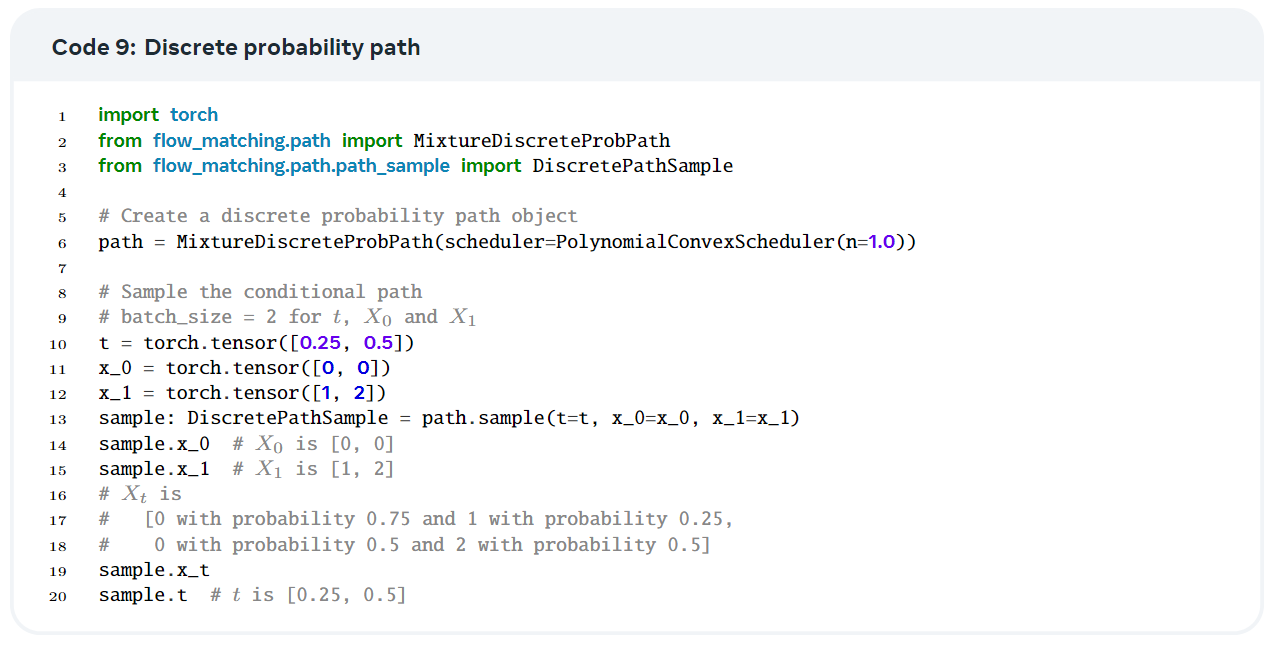
Code 9是混合路径的实现代码。

速率后验参数化

类比我们在FM²和扩散模型里面也会讲的多种预测方式，例如velocity-prediction、$x_0$-prediction、$x_1$-prediction，我们在DFM里面也可以使用类似的预测方式。

最简单的一种：使用神经网络预测公式9给出的分解条件速率$u_t^i(y^i,x^i\mid x_0,x_1)$，这就是velocity-prediction。

接下来介绍DFM里面的$x_1$-prediction，这个会稍微复杂一点。

根据我们在¹中证明出来的公式12，可以得到在$u_t^i(y^i,x^i\mid x_0,x_1)$取公式9的形式时，分解边缘速率为：

单独把第二个求和式拿出来，记为：

关于公式11中（*）步骤的详细说明：

\[\begin{aligned} p_{1\mid t}^i(x_1^i\mid x) &= \sum_{x_0,x_1^{\bar i}} p_{0,1\mid t}(x_0,x_1\mid x)\\ &\overset{拆开x_1}{=} \sum_{x_0,x_1^{\bar i}} p_{0,1\mid t}(x_0,x_1^{\bar i},x_1^i\mid x)\\ &\overset{\delta函数的性质}{=} \sum_{x_0,x_1^{\bar i}}\sum_{X_1^i}\delta(x_1^i,X_1^i) p_{0,1\mid t}(x_0,x_1^{\bar i},X_1^i\mid x)\\ &=\mathbb{E}\left[ \delta(x_1^i,X_1^i) \mid X_t = x \right] \end{aligned} \tag{12}\]

我们可以用神经网络去学习后验分布$p_{1\mid t}^{\theta,i}(x_1^i\mid x)$，$\theta$为神经网络的参数。这就是离散版的$x_1$-prediction。

这样理解：以文本为例，$x$是时间$t$时的“加噪”文本（但其实说“加噪“不准确，因为DFM的初始状态$x_0$是一个全mask的文本，$x$更类似一个处于中间状态的文本）。$x$作为神经网络的输入，神经网络预测$x_1^i$，$i\in [d]$表示这是$x_1$的第$i$个token，$d$为句长。神经网络一次预测所有token的单步变化概率，每个token共有$K$种变化情况（$K$为vocabulary的大小），神经网络的输出向量的维度就是$d\cdot K$。

混合路径的CDFM损失

我们基于$x_1$-prediction，即预测$p_{1\mid t}^{\theta,i}(x_1^i\mid x)$，继续讨论公式1所示混合路径情况下的CDFM损失。这里会有两种做法。

结合公式11，如果直接对比后验概率，则CDFM损失可以写为：

$\delta(\cdot,X_1^i)$，$p_{1\mid t}^{\theta,i}(\cdot\mid X_t)$都是概率质量函数，所以可以使用KL散度衡量二者之间的距离，即取Bregman散度为KL散度，得到：

这是第一种做法。

关于公式14的详细说明：

KL散度的公式是：$D(p,q)=\sum_{\alpha \in \mathcal{T}}p(\alpha)\log\cfrac{p(\alpha)}{q(\alpha)}$。在选择KL散度为Bregman散度后，公式13可以化为：

\[\begin{aligned} L_{CDFM}(\theta) &= \mathbb{E}_{t,X_0,X_1,X_t} \sum_{X_1^i} \delta(x_1^i,X_1^i) \log\cfrac{\delta(x_1^i,X_1^i)}{p_{1\mid t}^{\theta,i}( X_1^i\mid X_t)}\\ &=\mathbb{E}_{t,X_0,X_1,X_t} \sum_{X_1^i}\left[ \delta(x_1^i,X_1^i) \log{\delta(x_1^i,X_1^i)} - \delta(x_1^i,X_1^i) \log{p_{1\mid t}^{\theta,i}( X_1^i\mid X_t)}\right]\\ &= \text{const} - \mathbb{E}_{t,X_0,X_1,X_t} \sum_{X_1^i}\delta(x_1^i,X_1^i) \log{p_{1\mid t}^{\theta,i}( X_1^i\mid X_t)}\\ &\overset{\delta函数的性质}{=} \text{const} - \mathbb{E}_{t,X_0,X_1,X_t} \log{p_{1\mid t}^{\theta,i}(x_1^i\mid X_t)} \end{aligned} \tag{15}\]

第二种做法是使用¹中公式14所示的分解CDFM损失，如下：

取$Z=(X_0,X_1)$。使用该公式需要知道$u_t^{\theta,i}$，因为神经网络预测了$p_{1\mid t}^{\theta,i}$，所以$u_t^{\theta,i}$是能算出来的。

公式16中的Bregman散度可以选择广义的KL损失（其输入不一定要是概率分布）。具体而言，对于向量$u,v\in \mathbb R_{\ge 0}^{m}$，广义KL损失是：

这种选择下对应的Bregman散度为：

混合轨迹采样

我们在¹中的公式5已经给出per coordinate的采样方式，结合前面讨论的混合路径，采样公式可以写为：

在混合路径的特定情况下为：

在已知$X_t = x$的情况下，使用公式20进行采样的具体步骤如下：

1. 从$p_{1\mid t}^i(X_1^i\mid x)$采样出$X_1^i$，$X_1^i\sim p_{1\mid t}^i(X_1^i\mid x)$。$p_{1\mid t}^i(X_1^i\mid x)$是由模型预测得到。
2. 基于$X_t^i$更新出$X_{t+h}^i$。这一步需要使用⁴中公式9所示的Euler step，并将其中的速率设置为$\cfrac{\dot \kappa_t}{1 -\kappa_t}\left[\delta(y^i,X_1^i) - \delta(y^i,x^i)\right]$。这一步决定了$X_{t+h}^i=X_t^i$还是$X_{t+h}^i=X_1^i$。

单边混合路径和保概率速率

我们在第一次讲CTMC的那篇文章⁴里面的最后一部分讲了一下保概率速率，到这里终于要用到了。

简单回顾一下在CTMC模型里面讲到的保概率速率，它简单的说就是在已有的速率$u_t(y,x)$中加入另一个速率$v_t(y,x)$，只要$v_t(y,x)$是divergence-free的，那么$u_t(y,x)$生成概率路径不会改变。所谓divergence-free，指$\sum_x v_t(y,x)p_t(x) = 0$。

对DFM里面的分解条件概率路径$p_{t\mid Z}^i(x^i\mid z)$，其对应的保概率条件速率$v_t^i(y^i,x^i\mid z)$满足：

一般来说这个保概率条件速率$v_t^i(y^i,x^i\mid z)$不是特别好找到。但是如果我们能有如下两个假设：

1. iid的目标分布： $p(x) = \prod_i p(x^i)$。
2. 源分布和目标分布的数据独立配对：$\pi_{0,1}(x_0,x_1) = p(x_0)q(x_1)$。

那么保概率条件速率的解析式还是比较好找到的。接下来我们来构造这个保概率条件速率。

根据前面的两条假设，能写出混合路径的形式如下：

这个写法和我们前面的混合概率路径的写法的差异就是只用$x_1$作为条件，但其实它和用$x_0,x_1$都作为条件应该是等价的。

类比公式6

对比Kolmogorov方程，知道：

可见$u_t^i(y^i,x^i\mid x_1)$生成$p^i_{t\mid 1}(x^i\mid x_1)$。如果要找到对$p^i_{t\mid 1}(x^i\mid x_1)$而言divergence-free的条件速率，一个简单的技巧是找到一个和$u_t^i(y^i,x^i\mid x_1)$方向相反的条件速率⁵，这样在总时间范围内折两个速率差的散度和就是0，所以这两速率的差就是我们要找的divergence-free的条件速率，也就是保概率条件速率。记这个反向的条件速率为$\tilde u_t^i(y^i,x^i\mid x_1)$，它的形式应该是：

证明在⁵的E.5和E.6中。

所以divergence-free的速率是：

因为$v_t^i(y^i,x^i \mid x_1)$是divergence-free的，所以把它以任意比例加到原来的速率里面都不会影响生成的概率路径。所以公式10所示分解边缘速率如果改写成下面的形式：

不影响所生成的边缘概率路径。第二个等式是因为$u_t^i(y^i,x^i\mid x_1) =u_t^i(y^i,x^i\mid x_1^i)$，$v_t^i(y^i,x^i\mid x_1) =v_t^i(y^i,x^i\mid x_1^i)$。

那么，用公式27所示的速率进行采样的步骤是：

1. 从$p_{1\mid t}^i(X_1^i\mid x)$采样出$X_1^i$，$X_1^i\sim p_{1\mid t}^i(X_1^i\mid x)$。$p_{1\mid t}^i(X_1^i\mid x)$是由模型预测得到。

2. 基于$X_t^i$更新出$X_{t+h}^i$。这一步需要使用⁴中公式9所示的Euler step，并将其中的速率设置为

   \[u_t^i(y^i,x^i\mid x_1) = \cfrac{\dot \kappa_t}{1-\kappa_t}\left[\delta(y^i,X_1^i) - \delta(y^i,x^i)\right] +c_t\left[ \cfrac{\dot \kappa_t}{1-\kappa_t}\left[\delta(y^i,x_1^i) - \delta(y^i,x^i)\right] - \cfrac{\dot \kappa_t}{\kappa_t} \left[\delta(y^i,x^i) - p(x^i)\right] \right] \tag{28}\]

   其中$c_t>0$是与时间相关的常数。

在https://github.com/facebookresearch/flow_matching库里面实现的DFM的代码如下：

import torch  

from flow_matching.path import MixtureDiscreteProbPath, DiscretePathSample  
from flow_matching.path.scheduler import PolynomialConvexScheduler  
from flow_matching.loss import MixturePathGeneralizedKL  
from flow_matching.solver import MixtureDiscreteEulerSolver  
from flow_matching.utils import ModelWrapper  

# Define a trainable velocity model  
model = ...   

optimizer = torch.optim.Adam(model.parameters())  

scheduler = PolynomialConvexScheduler(n=1.0)  
path = MixtureDiscreteProbPath(scheduler=scheduler)  
loss_fn = MixturePathGeneralizedKL(path=path)  # Generalized KL Bregman divergence  

for x_0, x_1 in dataloader:  # Samples from π0,1 of shape [batch_size, *data_dim]  
    t = torch.rand(batch_size) * (1.0 - 1e-3)  # Randomize time t ∼ U [0, 1 − 10−3]  
    sample: DiscretePathSample = path.sample(t=t, x_0=x_0, x_1=x_1)  # Sample the conditional path  
    model_output = model(sample.x_t, sample.t)  

    loss = loss_fn(logits=model_output, x_1=sample.x_1, x_t=sample.x_t, t=sample.t)  # CDFM loss  

    optimizer.zero_grad()  
    loss.backward()  
    optimizer.step()  

class ProbabilityDenoiser(ModelWrapper):  
    def forward(self, x: torch.Tensor, t: torch.Tensor, **extras) -> torch.Tensor:  
        logits = self.model(x, t, **extras)  
        return torch.nn.functional.softmax(logits.float(), dim=-1)  

# Sample X1  
probability_denoiser = ProbabilityDenoiser(model=model)  
x_0 = torch.randint(size=[batch_size, *data_dim])  # Specify the initial condition  
solver = MixtureDiscreteEulerSolver(  
    model=probability_denoiser,  
    path=path,  
    vocabulary_size=vocabulary_size  
)  

step_size = 1 / 100  
x_1 = solver.sample(x_init=x_0, step_size=step_size, time_grid=torch.tensor([0.0, 1.0 - 1e-3]))

一个独立的DFM的代码案例如下：

import torch  
import matplotlib.pyplot as plt  
from torch import nn, Tensor  
from sklearn.datasets import make_moons  

class DiscreteFlow(nn.Module):  
    def __init__(self, dim: int = 2, h: int = 128, v: int = 128):  
        super().__init__()  
        self.v = v  
        self.embed = nn.Embedding(v, h)  
        self.net = nn.Sequential(  
            nn.Linear(dim * h + 1, h), nn.ELU(),  
            nn.Linear(h, h), nn.ELU(),  
            nn.Linear(h, h), nn.ELU(),  
            nn.Linear(h, dim * v)  
        )  

    def forward(self, x_t: Tensor, t: Tensor) -> Tensor:  
        return self.net(  
            torch.cat(  
                (t[:, None], self.embed(x_t).flatten(1, 2)), -1  
            )  
        ).reshape(list(x_t.shape) + [self.v])  

batch_size = 256  
vocab_size = 128  

model = DiscreteFlow(v=vocab_size)  
optim = torch.optim.Adam(model.parameters(), lr=0.001)  

for _ in range(10000):  
    x_1 = Tensor(make_moons(batch_size, noise=0.05)[0])  
    x_1 = torch.round(torch.clip(x_1 * 35 + 50, min=0.0, max=vocab_size - 1)).long()  
    x_0 = torch.randint(low=0, high=vocab_size, size=(batch_size, 2))  

    t = torch.rand(batch_size)  
    x_t = torch.where(torch.rand(batch_size, 2) < t[:, None], x_1, x_0)  

    logits = model(x_t, t)  
    loss = nn.functional.cross_entropy(logits.flatten(0, 1), x_1.flatten(0, 1)).mean()  
    optim.zero_grad()  
    loss.backward()  
    optim.step()  

x_t = torch.randint(low=0, high=vocab_size, size=(200, 2))  
t = 0.0  
results = [(x_t, t)]  
while t < 1.0 - 1e-3:  
    p1 = torch.softmax(model(x_t, torch.ones(200) * t), dim=-1)  
    h = min(0.1, 1.0 - t)  
    one_hot_x_t = nn.functional.one_hot(x_t, vocab_size).float()  
    u = (p1 - one_hot_x_t) / (1.0 - t)  
    x_t = torch.distributions.Categorical(probs=one_hot_x_t + h * u).sample()  
    t += h  
    results.append((x_t, t))  

fig, axes = plt.subplots(1, len(results), figsize=(15, 2), sharex=True, sharey=True)  
for (x_t, t), ax in zip(results, axes):  
    ax.scatter(x_t.detach()[:, 0], x_t.detach()[:, 1], s=10)  
    ax.set_title(f't={t:.1f}')  
plt.tight_layout()  
plt.show()

DFM生成效果如下：