离散型流匹配模型（2）

接着上一次学习的DFM的上半部分，这次学习DFM的下半部分。主要还是基于Flow Matching Guide and Code¹。

分解路径、速度和损失

在实际实现DFM的时候，我们会想要像FM²一样用神经网络预测上一节说的条件速度场，即$u^{\theta}_t(y,x) = \mathbb{E}[u_t(y,X_t\mid Z )\mid X_t =x )]$。但是，如果这样做，那么神经网络需要处理非常多种情况。具体而言，因为$y\in \mathcal{S}=\mathcal{T}^d$，其中$\mathcal{T} = {1,\cdots, K}$是vocabulary，$d$是句子长度，所以神经网络输出的大小为$K^d$（对第一个词要考虑$K$个状态，对第二个、第三个直到第$d$个词都要考虑$K$个状态，所以是$K^d$）。这么大的输出大小是不可实现的。为解决这个问题，可以使用分解（factorized）³方法。

下面要逐个使用这种方法来分解（边缘/条件）路径、（边缘/条件）速度和条件损失。

分解边缘速度

分解方法的核心思想在于：只考虑最多一个token的改变。因为多个token的改变可以视为逐个token的单步变化的叠加。探讨一个token的改变就像探讨基变换一样。

分解边缘速度的具体形式是：

\[u_t(y,x) = \sum_i \delta(y^{\bar{i}},x^{\bar{i}})u_t^i(y^i,x)\tag{1}\]

$\bar i = {1,\cdots, i-1,i+1,\cdots,d}$，就是把$i$去掉，相当于只考虑第$i$个token的变化。分解边缘速度如下图所示：

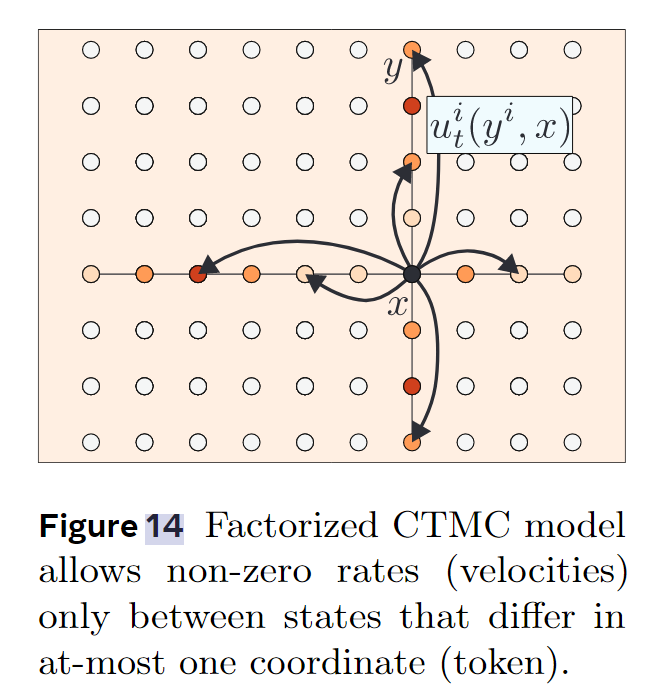
现在我们只需要使用模型预测$u_t^{i}(y^i,x)$了。其中，$i\in [d] = {1,\cdots,d}$，$y^i \in \mathcal{T}$是第$i$个token状态改变后所在的状态，$x\in \mathcal{S}$为状态转移之前的全部token的状态，$u_t^i(y^i,x) \in \mathbb R$是一个标量速率。所以，模型要输出的结果的维度是$d\cdot K$（总共$d$个token，每个token有$K$种可以改变到的状态，对应$d\cdot K$种速率），相比之前的$K^d$大大减小。

分解的边缘速率还是要满足速率条件，不过是要按照每个token的层级进行描述，如下：

\[u_t^i(y^i,x)\ge 0 \text{ for all } y^i \neq x^i \text{, and } \sum_{y^i \in \mathcal{T}}{u^i_t(y^i,x)} = 0 \quad \text{for all }x \in \mathcal{S} \tag{2}\]

$\forall i\in [d]$，公式（2）都要满足。

既然我们有了分解边缘概率，那么采样过程也可以coordinate-wise（逐维）地进行，代入公式（1）到CTMC模型的转移核之中，即：

\[\begin{aligned} \mathbb{P}(X_{t+h}=y\mid X_t = x)&=\delta(y,x)+hu_t(y,x)+o(h)\\ &\overset{代入公式(1)}{=} \delta(y,x)+h\sum_i \delta(y^{\bar{i}},x^{\bar{i}})u_t^i(y^i,x)+o(h)\\ &\overset{公式(4)}{=} \prod_{i}\left[ \delta(y^i,x^i) + h u_t^i(y^i,x) +o(h) \right] \end{aligned} \tag{3}\]

公式（3）第二个等号基于如下等式：

\[\prod_i\left[ a^i + h b^i \right] = \prod_i a^i + h\sum_{i}\left(\prod_{j\neq i}a^j\right) b^i + o(h) \tag{4}\]

取$a^i = \delta(y^i,x^i)$，$b^i = u_t^i(y^i,x)$，同时注意到$\prod_i \delta(y^i,x^i) = \delta(y,x)$，就得出了公式（3）中第二个等号表示的关系。

所以我们还可以用分解边缘速率定义一个分解转移核用以采样：

\[\begin{aligned} \mathbb{P}(X^i_{t+h}=y^i\mid X_t = x) &=\delta(y^i,x^i) + h u_t^i(y^i,x) +o(h) \\ \mathbb{P}(X_{t+h}=y\mid X_t = x) &=\prod_i\mathbb{P}(X^i_{t+h}=y^i\mid X_t = x) \end{aligned}\tag{5}\]

采样方法还是可以用CTMC模型里面说过的Euler法，但是这里是per coordinate的采样，即每一维单独进行采样。

其实FM的采样也可以写成类似的分解的形式，但一般不这么用。值得一提的是：FM的采样是确定性的，而DFM的采样具有随机性。

分解边缘概率路径

上面我们已经实现了分解边缘速度，现在考虑用一样的方法分解边缘概率路径$q_t(x)$：

\[q_t(x) = \prod_{i}q_t^i(x^i)\tag{6}\]

其中，$q_t^i(x^i)$就是分解后的边缘概率路径。

接下来我们想说明：分解边缘速率生成分解边缘概率路径时，非分解的边缘速率也能生成非分解的边缘概率路径，也就是希望边缘速率和边缘概率路径的关系在分解和非分解形式下都保留。具体而言就是如下命题：

命题2 令$q_t(x)$由公式（6）所示的分解形式定义，当$u_t^i(y^i,x^i)\in C([0,1))$能够生成$q_t^i(x^i)$时，那么$q_t$由如下分解形式的边缘速率生成：

\[u_t(y,x)=\sum_i\delta(y^{\bar i},x^{\bar i})u_t^i(y^i,x^i) \tag{7}\]

命题2的证明如下：

首先根据边缘概率的定义，我们可以得到$x^i$和$x^{\bar i}$的边缘概率可以通过如下方式计算（就是把无关的变量求和掉）：

\[q^i(x^i) := \sum_{x^{\bar i}}q(x) \quad q^{\bar i }(x^{\bar i }) :=\sum_{x^i} q(x) \tag{8}\]

推导如下：

\[\begin{aligned} \cfrac{\mathrm{d}}{\mathrm{d}t}q_t(y) &\overset{代入公式(6)}{=} \cfrac{\mathrm{d}}{\mathrm{d}t}\prod_i q_t^i(y^i)\\ &\overset{乘法求导法则}{=} \sum_i q^{\bar i}_t(y^{\bar i}) \cfrac{\mathrm{d}}{\mathrm{d}t}q_t^i(y^i)\\ &\overset{\text{Kolmogorov}方程}{=} \sum_i q^{\bar i}_t(y^{\bar i}) \left[ \sum_{x^i} u_t^i(y^i,x^i)q_t^i(x^i) \right]\\ &\overset{(*)}{=} \sum_i \left[ \sum_{x^{\bar i}}\delta(y^{\bar i}, x^{\bar i} ) q_t^{\bar i}(x^{\bar i}) \right] \left[ \sum_{x^i} u_t^i(y^i,x^i)q_t^i(x^i) \right]\\ &\overset{分配律}{=} \sum_i \sum_{x^{\bar i}}\sum_{x^i} \left[ \delta(y^{\bar i}, x^{\bar i} ) q_t^{\bar i}(x^{\bar i}) u_t^i(y^i,x^i)q_t^i(x^i) \right]\\ &\overset{合并x^i和x^{\bar i}}{=} \sum_i \sum_{x} \left[ \delta(y^{\bar i}, x^{\bar i} ) u_t^i(y^i,x^i)q_t(x) \right]\\ &\overset{交换求和顺序}{=} \sum_{x}\left[\sum_i \left[ \delta(y^{\bar i}, x^{\bar i} ) u_t^i(y^i,x^i) \right]q_t(x)\right]\\ \end{aligned} \tag{9}\]

（*）式基于$q_t^{\bar i }(y^{\bar i}) = \sum_{x^{\bar i}}\delta(y^{\bar i}, x^{\bar i})q_t^{\bar i}(x^{\bar i})$。根据最后结果，对比Kolmogorov方程，就知道$u_t(y,x)=\sum_i\delta(y^{\bar i},x^{\bar i})u_t^i(y^i,x^i)$了。

分解条件速率和条件概率路径

接下来我们还需要分解条件速率和条件概率路径。换句话说，我们希望得到分解版的离散边缘化技巧（Discrete Factorized Marginalization Trick）。

定理16（Discrete Factorized Marginalization Trick）考虑一个边缘概率路径通过如下方式构造：

\[p_t(x) =\sum_z p_{t\mid Z}(x \mid z) p_Z(z)\text{, with }p_{t\mid Z}(x\mid z)= \prod_ip_{t\mid Z}^i(x^i\mid z)\tag{10}\]

其中，$p_{t\mid Z}^i(x^i\mid z)$是分解条件概率路径，就像公式（6）中的分解边缘概率路径一样。

假设：$\forall x \in \mathcal{S}, \forall t\in[0,1)$， $p_t(x) > 0$。分解条件速率$u_t^{i}(y^i, x^i \mid z) \in C([0,1))$生成分解条件概率路径$p_{t\mid Z}^i(x^i\mid z) \in C^1([0,1))$。

假设满足时，边缘速率

\[u_t(y,x) =\sum_i\delta(y^{\bar i},x^{\bar i})u_t^i(y^i,x)\tag{11}\]

生成边缘概率路径$p_t(x)$。

其中

\[u_t^i(y^i,x)=\sum_z u_t^i(y^i,x^i\mid z)p_{Z\mid t}(z\mid x) = \mathbb{E} \left[ u_t^i(y^i,X_t^i\mid Z) \mid X_t = x \right]\tag{12}\]

定理16的证明如下

\[\begin{aligned} u_t(y,x) &\overset{(*)}{=}\sum_z u_t(y,x\mid z)p_{Z\mid t}(z\mid x)\\ &\overset{公式(7)}{=}\sum_z \left[ \sum_i\delta(y^{\bar i},x^{\bar i})u_t^i(y^i,x^i\mid z) \right] p_{Z\mid t}(z\mid x)\\ &\overset{交换求和顺序}{=}\sum_i \delta(y^{\bar i},x^{\bar i}) \underbrace{\left[ \sum_z u_t^i(y^i,x^i\mid z) p_{Z\mid t}(z\mid x) \right]}_{u_t^i(y^i,x)} \\ \end{aligned} \tag{13}\]

（*）步是我们在DFM上一节⁴中已经得到的结论。

那么根据（13）式，就知道公式（11）和（12）了。

接下来我们还要说明公式（11）表示的边缘速率能够生成边缘概率路径$p_t(x)$，这需要用到我们上一节⁴讲的离散边缘化技巧，离散边缘化技巧有使用的假设，即 $p_{t\mid Z}(x\mid z)\in C^{1}([0,1))$，$u_t(y,x\mid z)\in C([0,1))$。我们接下来说明这个假设能满足。

根据定理16的假设可知$p_{t\mid Z}^i(x^i\mid z) \in C^1([0,1))$，$\forall t \in C([0,1)), p_t(x) > 0$，所以根据$p_{t\mid Z}(x\mid z)=\prod_ip_{t\mid Z}^i(x^i\mid z)$可知$p_{t\mid Z}(x\mid z)\in C^1([0,1))$。根据定理16的假设可知$u_t^{i}(y^i, x^i \mid z) \in C([0,1))$，根据公式7我们知道$u_t(y,x\mid z)=\sum_i\delta(y^{\bar i},x^{\bar i})u_t^i(y^i,x^i\mid z)$，所以可以知道$u_t(y,x\mid z)\in C([0,1))$。

所以离散边缘化技巧假设满足，可以应用该技巧，得出

公式（11）表示的边缘速率$u_t(y,x)$能够生成边缘概率路径$p_t(x)$。

所以，定理16得到证明。

分解条件损失函数

我们可以让模型预测分解形式的速率$u_t^{\theta,i}$，替代原先预测非分解形式速率$u_t^{\theta}$的形式，那么条件损失函数的形式可以改写为：

\[L_{CDFM}(\theta) = \mathbb{E}_{t,Z,X_t\sim p_{t\mid Z}} \sum_i D_{X_t}^i \left( u_t^i(\cdot,X_t \mid Z), u_t^{\theta,i}(\cdot, X_t) \right) \tag{14}\]

其中，$t\in U[0,1]$，$u_t^{i}(\cdot,x\mid z), u_t^{\theta,i}(\cdot,x) \in \mathbb{R}^{\mathcal{T}}$。$u_t^{i}(\cdot,x\mid z),u_t^{\theta,i}(\cdot,x)$需要满足速率条件。$D_{x}^i(u,v)$是分解后的Bregman散度。

关于$u_t^{i}(\cdot,x\mid z),u_t^{\theta,i}(\cdot,x)$满足速率条件，可以用更形式化的方式表达：

定义： 对于$\alpha \in \mathcal{T}$，

\[\Omega_{\alpha} = \left\{ v \in \mathbb{R}^{\mathcal{T}}\mid v(\beta)\ge 0 \text{ }\forall\beta \in \mathcal{T}\backslash \{\alpha\}\text{, and } v(\alpha) = -\sum_{\beta\neq \alpha} v(\beta) \right\} \subset \mathbb{R}^{\mathcal{T}}\tag{15}\]

$\Omega_{\alpha}$显然是个凸集合。

形式化的说，$u_t^{i}(\cdot,x\mid z),u_t^{\theta,i}(\cdot,x)$满足速率条件，就是$u_t^{i}(\cdot,x\mid z),u_t^{\theta,i}(\cdot,x)\in \Omega_{x^i}$。

关于$D_{x}^i(u,v)$，在⁴中说过，它需要一个凸函数来定义。不过相比于非分解的$D_x(u,v)$，$D_{x}^i(u,v)$需要的也是一个分解的凸函数，可以记为$\Phi_x^i : \Omega_{x^i} \to \mathbb R$。

---